Researchers at the Université de Picardie Jules Verne in France and the University of Miskolc in Hungary use ArrayFire in the analysis and study of the dynamical properties of a nonlinear growth equation, as described in this paper.
Oftentimes, technical computing problems are simply intractable on CPUs and bigger devices like GPUs are required in order to get the job done. In this case, ArrayFire was an easy-to-use option for these researchers to build and analyze math quickly and efficiently on the GPU.
From their abstract: “The conserved Kuramoto-Sivashinsky equation is considered as the evolution equation of amorphous thin film growth in one- and in two-dimensions. The role of the nonlinear term and the properties of the solutions are investigated analytically and numerically. We provide analytical results on the wavelength and amplitude. We present numerical simulations to this equation which show the roughening and coarsening of the surface pattern and the evolution of the surface morphology in time for different parameter values in one- and in two-dimensions.”
The conserved Kuramoto-Sivashinsky equation analyzed takes the form of:
This equation has applications in molecular beam epitaxy (MBE) which is important in many industrial applications such as in the growth of nanostructure on crystal surfaces as the authors point out. For example, these methods are employed in the creation of transistors on silicon wafers.
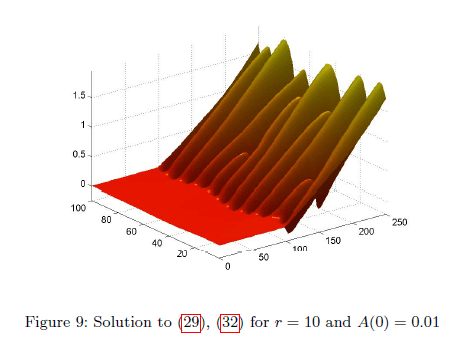
The researchers modeled this equation in one- and two-dimensions. Here are two figures from the paper that represent solutions to the equation for particular initial conditions and parameters.
In one-dimension,
And in two-dimension,
ArrayFire is used to model math equations all over the world due to its highly programmable interface and focus on rapid performance. We thank the authors for their contributions and great work in this space.